Stark Tables for Clearing the Lunar Distance

Stark Tables for Clearing the Lunar Distance
von Bruce Stark

Dieses Buch ist ein Kochbuch! Ein Kochbuch zur Ermittlung der Zeit am Nullmeridian, der Grundlage für die Bestimmung der geographischen Länge des Beobachtungsortes. Es steht in der Tradition von nautischen Hand- und Lehrbüchern über die Monddistanzen, die sich an die Praktiker richten, Kapitäne und Steuerleute, die weder an Mathematik noch an den Hintergründen der Methode interessiert sind, die oft nicht einmal die Fähigkeiten für die theoretische Durchdringung des Verfahrens besitzen. Ihr einziges Interesse ist die einfache, schnelle und zuverlässige Bestimmung der augenblicklichen Schiffsposition. Diese Tradition in der Beschreibung der Monddistanzen steht in erstaunlichem Kontrast zu den Lehrbüchern der früheren Navigationsschulen.

Die in der zweiten Hälfte des 18. Jahrhunderts in den Navigationsalltag Einzug haltenden Monddistanzen waren die Lösung für das bis dahin bestehende Unvermögen, die geographische Länge auf See zu bestimmen. In die Seefahrtsgeschichte ist dieses Problem als das sogenannte Längenproblem eingegangen. Um seine Lösung haben sich berühmte Köpfe von Galilei bis Newton ohne endgültigen Erfolg bemüht. Anders als bei der Längenbestimmung lagen die Verhältnisse bei der Ermittlung der geographischen Breite. Mit Hilfe der Höhenmessung von Gestirnen war die Seefahrt schon lange in der Lage, die Breite des Schiffsortes mit zufriedenstellender Genauigkeit zu ermitteln. Die Länge aber konnte immer nur durch Koppelrechnung vermutet werden, was insbesondere bei langen Reisen völlig unzureichend war. Deshalb wurde Breitennavigation betrieben. Die Schiffe steuerten die Breite des Bestimmungsortes an und segelten dann den Breitenkreis ab, bis das Ziel gefunden war.

Fast gleichzeitig wurden im 18. Jahrhundert zwei Lösungen für das Längenproblem gefunden. Die eine war die Entwicklung eines auch über lange Zeiträume und unter den harten Bedingungen des Seealltags hinlänglich genau gehenden Chronometers durch John Harrison. Verfügt man über die Zeit eines Vergleichsmeridians, zum Beispiel desjenigen von Greenwich, und vergleicht diese mit der astronomisch leicht zu ermittelnden lokalen Zeit, so kann aus der Zeitdifferenz auf die eigene Länge geschlossen werden. Diese Methode hatte allerdings einen gravierenden Nachteil: Chronometer waren zunächst äußerst rar und bis zum Ende des 19. Jahrhunderts sehr teuer, zu teuer für viele Kapitäne.

Die zweite Lösung für das Längenproblem waren die Monddistanzen, im nautischen Englisch gewöhnlich als Lunars bezeichnet. Der Winkel zwischen dem Mond und einem weiteren, geeignet gewählten Gestirn, die sogenannte Monddistanz, ändert sich mit ungefähr 12° am Tag, also einem halben Grad in der Stunde. Mit dieser relativ großen Änderungsrate des Winkels zwischen den beiden Himmelskörpern kann man aus der gemessenen Distanz ziemlich genau auf den Zeitpunkt der Messung schließen. Die Monddistanz ist bis auf gewisse, rechnerisch durchzuführende Korrekturen an allen Beobachtungspunkten der Erde gleich. Kennt man also für einen Vergleichsmeridian die Uhrzeit zu einem speziellen Wert der Monddistanz, den man gerade an Bord irgendwo auf den Weltmeeren gemessen hat, dann kann man aus der Differenz dieser Uhrzeit und der eigenen Ortszeit die Länge des Schiffsortes erschließen.

Die Idee war nicht neu, sie war mindestens seit dem 15. Jahrhundert im Umlauf. Was aber zunächst fehlte war neben einem Meßgerät zur genauen Messung der Distanz die Fähigkeit, die Monddistanzen ausreichend genau für einen Vergleichsmeridian vorherzuberechnen. Mit der Newtonschen Gravitationstheorie und den Arbeiten von Leonhard Euler wurde diese Aufgabe schließlich gelöst. Tobias Maier berechnete auf der Grundlage von Eulers THEORIA MOTUS LUNAE EXHIBENS OMNES EIUS INAEQUALITATES zur Mitte des 18. Jahrhunderts erstmals für die Zwecke der Navigation geeignete, ausreichend genaue Mondtafeln. Nevil Maskelyne, Astronomer Royal und Mitglied des britischen Board of Longitude, kommt das Verdienst zu, diese Tafeln für den Gebrauch auf See aufbereitet und ein praktisches Verfahren für die Anwendung der Monddistanzen publiziert zu haben.

Es verblieb allerdings ein entscheidender Nachteil, der nie vollständig überwunden wurde: das Verfahren zur Reduktion der scheinbaren auf die wahren Monddistanzen war langwierig und fehleranfällig. Seit seinem Erscheinen im 18. Jahrhunderts haben sich viele kluge Köpfe um die Aufbereitung des Formelwerks in eine möglichst einfach zu handhabende Form bemüht, um die Längenbestimmung auf See mit Hilfe der Monddistanzen praktikabel werden zu lassen. Darunter waren solche illustren Namen wie Maskelyne, Lyon, Dunthorne, Borda, La Caille, Witchell, Thomson oder Bowditch.

Mit der Vorlage seiner äußerst einfachen und sicheren Methode hat Bruce Stark dieser Liste seinen eigenen Namen hinzugefügt, 100 Jahre nachdem die Monddistanzen als Navigationsmethode auf den Achterdecks und Brücken der die Weltmeere durchpflügenden Schiffe ausgemustert worden sind. Und er ist mit seiner Methode bestimmt nicht der Geringste unter den aufgezählten Größen. Die hier besprochenen Stark Tables enthalten das Werkzeug, gemessene Monddistanzen nach Starks eigener Methode in GMT, oder besser gesagt: in UT1 umzuwandeln. Das ist der entscheidende Schritt auf dem Wege zur Ermittlung der Länge für den Beobachtungsort.

Wie bereits am Anfang der Rezension festgestellt, bei dem vorliegenden Band handelt es sich um ein Kochbuch. Wer also von dem Buch erwartet, etwas über die Grundlagen der Monddistanzenmethode oder gar über die Ableitung von Formeln zu finden, der ist mit dem Erwerb des Buchs schlecht beraten. Die Mathematik hinter den Tabellen bleibt vollständig unerwähnt, man muß (und kann!) der Anleitung und den Tabellen ohne Prüfung vertrauen, so wie es die Seeleute vor der Einführung von über den Äther verbreiteten Zeitsignalen und vor der Verfügbarkeit von halbwegs preiswerten Chronometern mit den damaligen Tafelwerken auch getan haben.

Das Fehlen der Theorie tut dem Buch aber keinen Abbruch. Jeder, der seine Fertigkeiten im Umgang mit dem Sextanten verbessern will, der einen Eindruck gewinnen will, wie die Seeleute des späten 18. und des 19. Jahrhunderts navigiert haben, oder der tatsächlich einmal auf See seine Länge auf diese traditionelle Art und Weise bestimmen will, ist mit dem Buch richtig bedient.

Die Stark Tables sind kein Buch im eigentlichen Sinne, sondern, wie schon der Titel vermuten läßt, ein mit einigen Seiten Erläuterungen und wenigen Formblättern versehenes Tabellenwerk. Aber damit versetzt es den Benutzer in die Lage, ohne alle weiteren Hilfsmittel - Nautisches Jahrbuch oder Nautical Almanac, Sextant und Stoppuhr ausgenommen - die Länge des Beobachtungsortes zu bestimmen; je nach Fertigkeit mehr oder weniger genau. Beim Anfänger eher weniger genau, selbst wenn er schon einige Höhenmessungen von Gestirnen auf See hinter sich hat. Abweichungen in der Länge von mehr als einem Grad zwischen der ermittelten und der wahren Position bei den ersten Versuchen sollten nicht zur Resignation führen. Im Gegensatz zur Standlinie nach dem Verfahren von St. Hilaire bedeutet bei den Monddistanzen eine Meßungenauigkeit von einer Bogenminute keinen Fehler von einer Seemeile, sondern von 30 Bogenminuten. Je nach geographischer Breite sind das 20 bis 30 Meilen. Die starke Abhängigkeit des Fehlers in der Länge in Abhängigkeit von der Genauigkeit der Messung ist nicht der speziellen Methode zur Aufbereitung der Monddistanzen geschuldet, sondern liegt in der Sache selber. Hier gilt ganz besonders, nur Übung macht den Meister.

Mit seiner scharfsinnigen und für die Anwendung zweckmäßig aufbereiteten Methode lassen sich die mit dem Sextanten gemessenen Werte vergleichsweise schnell und sehr sicher in UT1 umwandeln. Auch ein wenig erfahrener Anwender des Verfahrens wird mit Starks Buch die UT1 aus seinen Höhenmessungen für Mond und Distanzgestirn und aus der gemessenen Distanz zwischen den Rändern der beiden Himmelskörper in weniger als einer halben Stunde ermittelt haben. Das ist bei Anwendung der klassischen Methoden rekordverdächtig. Man kann nur mutmaßen, daß Starks spezielle Aufbereitung der Monddistanzenmethode, eineinhalb Jahrhunderte früher erschienen, viele Anhänger unter den Navigatoren der klassischen Seefahrt gefunden hätte.

Es gibt zwei prinzipielle Klassen von Methoden zur Reduktion der scheinbaren auf die wahre Monddistanz, die strikten und die Näherungsmethoden. Starks Methode gehört zu den strikten Methoden. Die Formeln, die Stark seinen Tabellen und seinen Formblättern zugrundelegt, beruhen ganz wesentlich auf der fast durchgehenden Anwendung des Semiversus. Als weitere trigonometrische Funktion kommt der Kosinus nur ganz am Rande vor. Das reduziert die Zahl der notwendigen Tafeln. Darüber hinaus ist der Semiversus in Bezug auf die Zahl der notwendig zu berücksichtigenden Stellen in den Logarithmentafeln den anderen trigonometrischen Funktionen überlegen. Er ist symmetrisch in seinem Argument, so daß das Vorzeichen des Arguments unberücksichtigt bleiben kann. Und er ist immer positiv. Keine Vorzeichendiskussionen sind nötig und, was viel wichtiger ist, keine Vorzeichenfehler sind möglich.

Wer heute über die Monddistanzen die Länge des Beobachtungsortes bestimmen will, hat es schwerer als die Seeleute des 19. Jahrhunderts: die nautischen Jahrbücher enthalten seit dem Beginn des vergangenen Jahrhunderts nicht mehr die damals im 3-Stunden-Abstand tabellierten, vorherberechneten Monddistanzen, die dem Vergleich mit der gemessenen Monddistanz zur Ermittlung der GMT dienen. Stark löst diese Schwierigkeit mit einem kleinen Formblatt, mit dem in wenigen Minuten aus den den nautischen Jahrbüchern für die beiden beteiligten Himmelskörper entnommenen Größen Deklination und Greenwicher Stundenwinkel die früher tabellierte Distanz errechnet werden kann.

Das Ziel von Bruce Stark war, mit dem vorliegenden Band ein selbstkonsistentes Tabellenwerk zu erstellen, mit dem in einfacher Weise, ohne die Verwendung von irgendwelchen elektronischen Hilfsmitteln, die geographische Länge ermittelt werden kann. Halt! Schon der Titel STARK TABLES FOR CLEARING THE LUNAR DISTANCE AND FINDING UNIVERSAL TIME BY SEXTANT OBSERVATION beschränkt das Ziel des Werkes auf die Ermittlung der Zeit von Greenwich. Und das ist schade, damit fehlt dem Buch die Vollendung. Die Kenntnis der Zeit am Nullmeridian ist ja kein Ziel an sich. Der Wert der gefundenen Zeit liegt in der Möglichkeit, mit ihr die Länge des Positionsortes zu ermitteln. Und diesen letzten, kleinen Schritt geht Stark leider nicht.

Die geographische Länge ist die Differenz aus der mittleren Ortszeit und der durch die Monddistanzen ermittelten UT1. Es fehlt also zur Längenbestimmung noch die Ortszeit. Deren Ermittlung war Alltagsgeschäft der Navigatoren vor der Einführung elektromagnetisch übermittelter Zeitsignale. Zur Ermittlung der wahren Ortszeit ist nur die Höhe eines Gestirns, möglichst weit vom Meridian entfernt, erforderlich. In aller Regel ist die Höhe bereits ein Nebenprodukt der Monddistanzmessung. Die Berechnung der wahren Ortszeit aus der Höhe ist mit den Tabellen des Buches leider nur fast möglich. Zur vollständigen Berechnung hätte gereicht, dem Buch zu seinen 315 Seiten weitere 34 Seiten zu spendieren und die Tabelle log Dec über den abgedruckten Bereich von 0° bis 30° hinaus auf 90° zu erweitern.

Im Besitz der wahren Ortszeit muß darauf nur noch die im Nautischen Jahrbuch und im Nautical Almanac abgedruckte Zeitgleichung angewendet werden, um die mittlere Ortszeit zu bestimmen. Die Differenz aus der mittleren Ortszeit und der zuvor bestimmten UT1 umgerechnet in Grad ist die Länge des Beobachtungsortes. Der Rezensent hat für diesen Zweck ein Formblatt auf der Basis der Stark-Tabellen gestaltet und hier abgelegt, mit dem dieser letzte Schritt zur Ermittlung der Länge vollzogen werden kann. Dort wo Werte größer als 30° in der Tabelle log Dec verlangt sind, die Stark Tables also keine Auskunft mehr geben, dort muß man sich mit dem Taschenrechner behelfen und |log(cos x)| selbst berechnen.

Stark sieht in seiner Methode ein praktikables Backup zu den modernen elektronischen Systemen der Navigation. Soweit wollen wir ihm nicht folgen, insbesondere weil der letzte Schritt zur Ermittlung der geographischen Länge fehlt. Aber seine Methode, seine Tafeln sind sicher ein Mittel um - der Untertitel INCLUDING A CONVENIENT WAY TO SHARPEN CELESTIAL NAVIGATION SKILLS WHILE ON LAND verspricht es – die Fähigkeiten in der astronomischen Navigation zu festigen. Jeder, der Interesse an der astronomischen Navigation hat, wird seine Freude an dem Buch und der Anwendung der Monddistanzen haben. Es versetzt ihn in die Lage, wie die alten Seefahrer nur mit Papier und Bleistift versehen, die Monddistanzen auszuwerten. Und vielleicht verleitet das vorliegende Werk seinen Leser zum tieferen Einstieg in die Theorie und in die Geschichte dieser faszinierenden Methode zur Positionsbestimmung.

Anhang

Als Anhang zu dieser Rezension und als Erläuterung für den Besitzer der Stark Tables seien kurz die dem Verfahren zugrundeliegenden Formeln und die in dem Tabellenwerk enthaltenen Tabellen und Formblatter besprochen.

Formeln

Da die vorberechneten Monddistanzen im Nautical Almanac seit 1906 und im nautischen Jahrbuch seit den Jahren des ersten Weltkrieges nicht mehr veröffentlicht werden, müssen diese heute selbst berechnet werden. Stark legt dieser Berechnung das Law of Haversines zugrunde, eine mit dem Semiversus geschriebene Form des Seitenkosinussatzes:

Dabei ist D die wahre Monddistanz, weiter gehen der Greenwicher Stundenwinkel (GHA) für den Mond und das Distanzgestirn und die Deklination für beide Himmelskörper in die Formel ein.

Die Reduktion der scheinbaren auf die wahre Monddistanz erfolgt mit einer auf den Semiversus umgestellten Version der Formel von Dunthorne (1766):

Tabellen

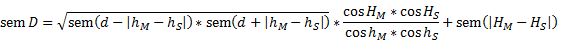
Folgende Tabellen enthalten die Stark Tables:

• Wrong Way Tables zur Ermittlung der scheinbaren Höhen aus den dem Nautischen Jahrbuch entnommenen wahren Höhen.

• Gesamtbeschickung für Kimmtiefe und Halbmesser von Mond und ggf. Sonne.

• Parallaxe – Refraktion für den Mond in Abhängigkeit von der scheinbaren Mondhöhe. Die Tabelle enthält gleichzeitig die Werte für die logarithmische Differenz.

• Refraktion – Parallaxe für das Distanzgestirn in Abhängigkeit von dessen scheinbarer Höhe. Dabei gibt es wegen der unterschiedlichen Parallaxe je eine Spalte für die Sonne, für die Planeten Venus oder Mars und für die Fixsterne bzw. die Planeten Jupiter oder Saturn. Ebenfalls in der Tabelle sind die Werte für die logarithmische Differenz des Distanzgestirns enthalten. Zur Vereinfachung der Rechnung sind die Werte für die logarithmische Differenz um ungefähr 0,000122 reduziert. Dadurch verschwindet dieser Wert für die Fixsterne über weite Höhenbereiche. Zum Ausgleich ist derselbe Wert auch bei der zugehörigen logarithmischen Differenz des Mondes abgezogen.

• Durch die Parallaxe vergrößerter Mondhalbmesser in Abhängigkeit von Horizontalparallaxe und scheinbarer Höhe.

• Sonnenhalbmesser in Abhängigkeit vom Datum.

• Verringerung des Halbmessers von Mond und Sonne durch Refraktion zur Korrektur der Distanz zwischen den Rändern der Himmelskörper auf die Mittelpunktsdistanz.

• K-Zahl für die Winkel zwischen 0° und 180°. Bei der K-Zahl handelt es sich um den Absolutbetrag des logarithmierten Semiversus.

• Tabellierung des Gaußschen Logarithmus log(x+1). Tatsächlich wird nicht der echte Gaußsche Logarithmus tabelliert, sondern

  

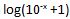
• Tabelle für den Absolutwert des logarithmierten Kosinus im Bereich zwischen 0° und 30°.

• Proportionallogarithmus plg = log(240‘) – log(x [‘]) zur Ermittlung der GMT für den Bereich zwischen 0 und 4 Grad.

• Proportionallogarithmus plg = log(3600 sec) – log(x[sec]) zur Ermittlung der GMT für den Bereich zwischen 0 und 60 Zeitminuten.

• Proportionallogarithmus plg = log(10800) – log(x) für den Bereich zwischen 0 und 3 Stunden bzw. 0 und 3 Grad.

Formblätter

Für die praktische Berechnung liefert das Buch drei Formblätter:

• zur Interpolation der Höhen auf den Zeitpunkt der Monddistanzenmessung,

• zur Reduktion der scheinbaren auf die wahre Monddistanz,

• zur Vorherberechnung der Monddistanz und zur Ermittlung der GMT mit Hilfe der ermittelten wahren Monddistanz.